PREDICTIVE ANALYTICS FOR THE ENERGY SECTOR

 

Machine Learning Business Use Case

One of the major areas where AIML can truly change the landscape is the energy sector. Let us first understand the “Analytics Maturity Model” before attempting to consider the implications:

Almost all the OEMs and principals of the energy sector have in-built objective analytics (e.g. enterprise pipeline management solution) along with ICS / DCS since ages that address the essential process requirements like vibration monitoring, condition monitoring, cathodic protection etal. pertaining to asset integrity. Then, we also have the major players that have developed real-time monitoring solutions in pace with the 4^th industrial revolution viz. advanced telemetry, imaging systems, distributed monitoring systems (vibration, acoustics, temperature), etc. However, when it comes to predictive analytics there is a huge gap since it is mostly done in hind-sight and is not real-time. There are very few players in the market who have indeed rolled-out real-time predictive analytics either as a SaaS model or a standalone offering. The GTM feasibility of many other similar products is underway as the global MLaaS market is forecasted to reach USD 117.19 billion by 2027 (source: https://www.fortunebusinessinsights.com/machine-learning-market-102226).   

Use-case Scenario

For the energy sector, there can be several use-case scenarios as listed below:

•  Process Optimization
•  Reducing MTBF / MTTR
•  Loss Prevention (process losses, leakages, etc.)

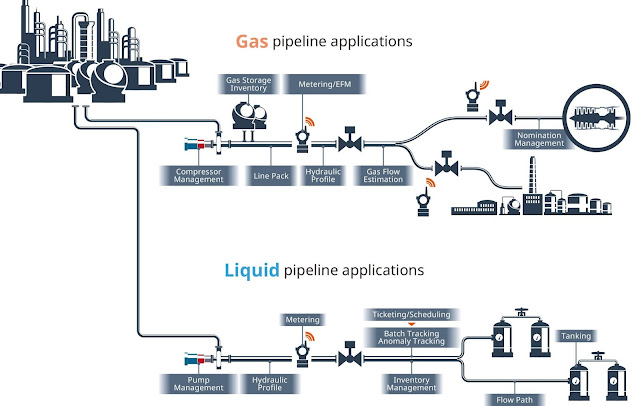
Here, I will attempt to present a use case scenario for “real-time predictive analytics” for a typical natural gas pipeline. A typical high-level production process flow is given below:

 

In this example, let us presume that we have a simple process flow for pipeline data management as shown below:

Data Scientists / Analysts must be aware of the entire data science life-cycle before attempting to initiate the solution as shown below:

Once the logged data is collected, the machine learning process is initiated as per the process flow shown below:

It is to be noted that supervised learning models are preferred since OEM design parameters need to be considered for baseline / target values. However, semi-supervised algorithms may be used while using a classification approach to get better results.

Building the model

Remember that the processed data will be humongous with hundreds of columns to accommodate all the relevant parameters collected via numerous sensors required to maintain pipeline integrity. Here, I will be focusing only on semi-supervised graph-based algorithms that can be validated and finally selected for deployment. For ease of business, I’m only considering distributed temperature monitoring dataset in this case.

Label Spreading

It is based on the normalized graph Laplacian:

This matrix has each a diagonal element l_ii equal to 1, if the degree deg(l_ii) > 0 (0 otherwise) and all the other elements equal to:

The behavior of this matrix is analogous to a discrete Laplacian operator, whose real-value version is the fundamental element of all diffusion equations. To better understand this concept, let's consider the generic heat equation:

This equation describes the behavior of the temperature of a pipeline section when a point is suddenly heated. From basic physics concepts, we know that heat will spread until the temperature reaches an equilibrium point and the speed of variation is proportional to the Laplacian of the distribution. If we consider a bidimensional grid at the equilibrium (the derivative with respect to when time becomes null) and we discretize the Laplacian operator (∇² = ∇ * ∇) considering the incremental ratios, we obtain:

Therefore, at the equilibrium, each point has a value that is the mean of the direct neighbors. It's possible to prove the finite-difference equation has a single fixed point that can be found iteratively, starting from every initial condition. In addition to this idea, label spreading adopts a clamping factor α for the labeled samples. If α=0, the algorithm will always reset the labels to the original values (like for label propagation), while with a value in the interval (0, 1], the percentage of clamped labels decreases progressively until α=1, when all the labels are overwritten.

The complete steps of the label spreading algorithm are:

•         Select an affinity matrix type (KNN or RBF) and compute W
•         Compute the degree matrix D
•         Compute the normalized graph Laplacian L
•         Define Y⁽⁰⁾ = Y
•         Define α in the interval [0, 1]
•         Iterate until convergence of the following step –

It's possible to show that this algorithm is equivalent to the minimization of a quadratic cost function with the following structure:

The first term imposes consistency between original labels and estimated ones (for the labeled samples). The second term acts as a normalization factor, forcing the unlabeled terms to become zero, while the third term, which is probably the least intuitive, is needed to guarantee geometrical coherence in terms of smoothness.

Python code for Label Spreading

We can test this algorithm using the Scikit-Learn implementation. Let's start by creating a very dense dataset:

from sklearn.datasets import make_classification

nb_samples = 5000 nb_unlabeled = 1000

X, Y = make_classification(n_samples=nb_samples, n_features=2,

n_informative=2, n_redundant=0, random_state=100)

Y[nb_samples - nb_unlabeled:nb_samples] = -1

We can train a LabelSpreading instance with a clamping factor alpha=0.2. We want to preserve 80% of the original labels but, at the same time, we need a smooth solution:

from sklearn.semi_supervised import LabelSpreading

ls = LabelSpreading(kernel='rbf', gamma=10.0, alpha=0.2)

ls.fit(X, Y)

Y_final = ls.predict(X)

The result is shown, as usual, together with the original dataset:

As it's possible to see in the first figure (left), in the central part of the cluster (x [-1, 0]), there's an area of circle dots. Using a hard-clamping, this aisle would remain unchanged, violating both the smoothness and clustering assumptions. Setting α > 0, it's possible to avoid this problem. Of course, the choice of α is strictly correlated with each single problem. If we know that the original labels are absolutely correct, allowing the algorithm to change them can be counterproductive. In this case, for example, it would be better to preprocess the dataset, filtering out all those samples that violate the semi-supervised assumptions. If, instead, we are not sure that all samples are drawn from the same pdata, and it's possible to be in the presence of spurious elements, using a higher α value can smooth the dataset without any other operation.

Similarly, one can also use “Label Propagation based on Markov Random Walks” to find the probability distribution of target labels for unlabeled samples given a mixed dataset by simulation of stochastic process.

It is to be noted that the above two algorithms can be applied against design parameters adjusted against the best achieved values based on historical data. In any other scenario, the predictions may go totally wrong since the iterations are based on absolute correctness of the labels (e.g. derived from control limits or stability tests).

Once the model has been validated with good level of accuracy and deployed for production, the ICS (Industrial Control System) interface (API integration) for real-time predictive analytics can be set-up that will trigger alarms at the set control points and provide deeper insights for loss prevention. As the ML system matures over time, one may even be able to move to the next level i.e. “Prescriptive Analytics”.

Conclusion

Given below is a estimated annual cost for the minimum length (100 km) and minimum diameter (12 inch) of a large company:

Component	Segment A (small)	Segment B (large)	Total
Periodic Inspection	$ 121550	$ 297000	$ 418550
Scheduled Pigging	$ 40000	$ 80000	$ 120000
Leak Surveys (@95% of total)	$ 13000	$ 22000	$ 35000
Repair Backlog (@annual cost of rule)	$ 103000	$ 197000	$ 300000
Total	$ 277550	$ 596000	$ 873550

Source: Greene’s Energy Group, LLC (2013), updated to 2015 dollars using the Bureau of Labor Statistics US All City Average Consumer Price Index (2013=233.5; 2015=237.8).

Note: The above table is a simplified one and does not include several factors like terrain, regulated / unregulated, mobilization costs, compliance costs, etc.

Cost-benefit Analysis

It is to be noted that even a 1% of loss prevention against an average production of 6 MMSCFD (169512.82 m3/d or 1066203.53 bbl/d) goes a long way in cost optimization for an oil & gas producer.

For this particular example, a savings of US$ 5400 / km can be easily achieved for a combined loss prevention strategy (gathering / process loss & maintenance / inspection cost).

Note: The above is a highly conservative estimate and actual savings may be 4x higher in actual practice. 

Reference Standards: ISO 55001:2014 Asset Management, ISO 31000:2018 Risk Management, ISO 14224:2006 Petroleum, petrochemical and natural gas reliability & maintenance, ISO/IEC CD 22989 AI Terms & Concepts, ISO/IEC AWI TR 5469 AI Functional Safety